1. Các công thức giải bất phương trình chứa căn
Ta có công thức giải bất phương trình chứa căn như sau:
Công thức 1:
$sqrt{f(x)} < g(x) Leftrightarrow left{begin{matrix}f(x) geq 0 g(x)geq 0 f(x) < g^{2}(x) end{matrix}right.$
Hoặc nếu có dấu bằng thì ta có:
$sqrt{f(x)} leq g(x) Leftrightarrow left{begin{matrix}f(x) geq 0 g(x)geq 0 f(x) leq g^{2}(x) end{matrix}right.$
Ví dụ: Giải bất phương trình: $sqrt{x}+sqrt{y-1}+sqrt{z-2}=frac{1}{2}(x+y+z)$
Giải:
ĐK: $xgeq 0; ygeq 1; zgeq 2$
Phương trình tương đương:
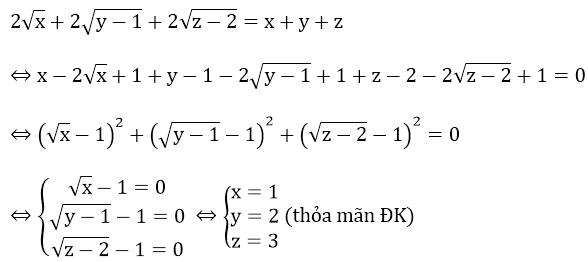
Công thức 2:
Hoặc trường hợp có thêm dấu bằng thì ta có:
Ví dụ: Giải bất phương trình: $x^{2}+9x+20=2sqrt{3x+10}$
ĐK: x$ frac{-10}{3}$

=> Nghiệm của bất phương trình x= -3
Đăng ký ngay để được các thầy cô ôn tập và xây dựng lộ trình học tập THPT vững vàng

2. Một số cách giải chi tiết bất phương trình chứa căn bậc hai
2.1. Phương trình và bất phương trình chứa căn thức cơ bản
Ví dụ 1: Giải các bất phương trình sau:
$sqrt{x^{2}-x-12}=7-x$
Giải:
$Rightarrow$ Nghiệm của phương trình là: $x=frac{61}{13}$
Ví dụ 2: Tìm tập nghiệm của bất phương trình sau: $sqrt{x-3}<2x-1$
Giải:
$Rightarrow$ Nghiệm của bất phương trình $S=[3,infty)$
2.2. Quy phương trình chứa căn thức về hệ phương trình không chứa căn thức
Sử dụng phương pháp đặt phụ ta quy phương trình căn thức về hệ phương trình không chứa căn thức. Ta có ví dụ sau đây:
Ví dụ: Giải phương trình sau: $sqrt[3]{x-2}+sqrt[3]{x+3}=sqrt[3]{2x+1}$ (1)
Giải:

Vậy (1) có các nghiệm $x=2; x=-3; x=frac{-1}{2}$
Ví dụ 2: Giải phương trình sau: $2(x^{2}+2)=5sqrt{x^{3}+1}$
Giải:

2.3. Sử dụng phương trình tương đương hoặc hệ quả
Ví dụ 1: Giải phương trình sau: $sqrt[3]{2x-1}+sqrt[3]{x-1}=sqrt[3]{3x+1}$ (1)
Giải:
Ví dụ 2: Giải phương trình sau: $sqrt{2x+3}+sqrt{x+1}=3x+2sqrt{2x^{2}+5x+3}-16$ (1)
Giải:
Đặt $u=sqrt{2x+3}+sqrt{x+1}geq 1$
Ta có $Leftrightarrow u^{2}=3x+4+2sqrt{2x^{2}+5x+3}$ với $ugeq 1$ (2)
Thay (1) vào (2) ta có phương trình hệ quả sau:
$u^{2}-20=uLeftrightarrow u^{2}-u-20=0$
$Leftrightarrow u=5$ hoặc $u=-4 Leftrightarrow u=5$ (do $ugeq 0$)
Từ (1) dẫn đến phương trình hệ quả:
Ta thay x = 3 vào (1) sẽ có kết quả đúng nên (1) sẽ có nghiệm x = 3
2.4. Sử dụng phương pháp chiều biến thiên hàm số
Ví dụ 1: Giải phương trình sau: $x^{5}+x^{3}-sqrt{1-3x}+4=0$ (1)
Giải:
Đặt $f(x)=x^{5}+x^{3}-sqrt{1-3x}+4$ với $xleq frac{1}{3}$
Khi đó (1) có dạng f(x) = 0 và miền xác định $xleq frac{1}{3}$
Ta có $f'(x)=5x^{4}+3x^{2}+frac{3}{2sqrt{1-3x}}>0, forall , x leq frac{1}{3}$
Vậy f(x) chính là hàm số đồng biến khi $x<frac{1}{3}$
Ta có $f'(-1)=0$ vậy $x=-1$ là nghiệm duy nhất của (1)
Ví dụ 2: Giải phương trình: $sqrt{x^{2}+15}=3x-2+sqrt{x^{2}+8}$ (1)
Giải:
Ta viết (1) dưới dạng $f(x)=3x-2+sqrt{x^{2}+8}-sqrt{x^{2}+15}=0$ (2)
Hàm số f(x) xác định với $forall x epsilon R$. Xét phương trình với 2 khả năng sau:
$Rightarrow x=1$ là nghiệm duy nhất của (1)
2.5. Phương pháp đánh giá hai vế
Với phương trình $f(x)=g(x), xin D$ ta có tính chất:
$f(x)geq A , forall , x in D$ hoặc $g(x)geq A , forall , x in D$
Khi đó: $f(x)=g(x) Leftrightarrow f(x)=A$ hoặc $g(x)=A$
Để bất đẳng thức $f(x)geq A; g(x)leq A; forall x in A$ ta áp dụng các kiến thức về bất đẳng thức.
Ví dụ 1: Giải phương trình sau: $sqrt{x-2}+sqrt{4-x}=x^{2}-6x+11$ (1)
Giải:
Ta có miền xác định (1) là $D=left { {x:2leq x leq 4} right }$
Ta có $x^{2}-6x+11=(x-3)^{2}+2geq 2, forall x epsilon D$ thì $f^{2}(x)=2+2sqrt{(x-2)(4-x)}leq 2+[(x-2)+(4-x)]=4$
Do đó $f(x)geq 0$ khi $forall x in D Rightarrow f(x)leq 2 , forall x, in D$
$Rightarrow x^{2}-6x+11=2Leftrightarrow x=3$
Hoặc $sqrt{x-2}+sqrt{4-x}Leftrightarrow x-2=4-x Leftrightarrow x=3$
$Rightarrow x=3$ nghiệm duy nhất của (1)
Ví dụ 2: Giải phương trình:
$sqrt{3x^{2}+6x+7}+sqrt{5x^{2}+10x+14}=4-2x-x^{2}$

2.6. Bất phương trình chứa căn thức có tham số
Ví dụ 1: Giải phương trình: $sqrt{x-4a+16}+2sqrt{x-2a+4}+sqrt{x}=0$
Giải:

Ví dụ 2: Giải và biện luận phương trình:
$sqrt{x^{2}+x+frac{m^{2}}{(x-1)^{2}}=x-frac{m}{x-1}}$ (1)
Giải:
Tham khảo thêm:
⭐Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết
Sau bài viết này, hy vọng các em đã nắm chắc được toàn bộ lý thuyết, công thức về bất phương trình chứa căn lớp 10, từ đó vận dụng hiệu quả vào bài tập. Ngoài ra để luyện tập thêm các em có thể truy cập ngay Vuihoc.vn và đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ để chuẩn bị tốt nhất cho kỳ thi đại học sắp tới nhé!


