Inverse Trig Derivatives

Inverse trig derivatives are the derivatives of inverse trigonometric functions. We have 6 inverse trigonometric functions that are the inverses of the 6 basic trigonometric functions. The inverse trig derivatives are defined only in the domain of the inverse trigonometric functions which are stated as follows:

Inverse Trigonometric Function Domain arcsin x [-1, 1] arccos x [-1, 1] arctan x R arccsc x (-∞, -1] U [1, ∞) arcsec x (-∞, -1] U [1, ∞) arccot x R

Let us learn the derivatives of inverse trigonometric functions with detailed proof. Also, let us solve a few problems related to the inverse trig derivatives.

1. What are Inverse Trig Derivatives? 2. Derivatives of Inverse Trig Functions 3. Inverse Trig Derivatives Proofs 4. Inverse Trig Derivatives and Integrals 5. FAQs on Inverse Trig Derivatives

The inverse trig derivatives are the derivatives of the inverse trigonometric functions arcsin (or sin-1), arccos (or cos-1), arctan (or tan-1), etc. We use implicit differentiation to find the derivatives of the inverse trig function which we we explore in detail in the upcoming section. Here are the inverse trig derivatives:

• The derivative of arcsin x is d/dx(arcsin x) = 1/√1-x², when -1 < x < 1
• The derivative of arccos x is d/dx(arccos x) = -1/√1-x², when -1 < x < 1
• The derivative of arctan x is d/dx(arctan x) = 1/(1+x²), for all x in R
• The derivative of arccsc x is d/dx(arccsc x) = -1/(|x|√x²-1), when x < -1 or x > 1
• The derivative of arcsec x is d/dx(arcsec x) = 1/(|x|√x²-1), when x < -1 or x > 1
• The derivative of arccot x is d/dx(arccot x) = -1/(1+x²), for all x in R

We know that another form of writing an inverse trig function, say arcsin x, is sin-1x. The derivatives of inverse trig functions can be written in alternative notation as follows:

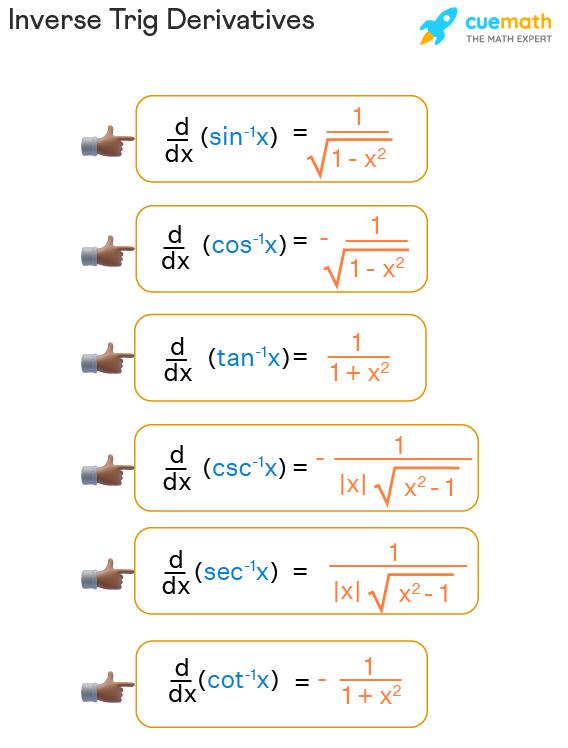
1. d/dx (sin-1x) = 1/√1-x²
2. d/dx(cos-1x) = -1/√1-x²
3. d/dx(tan-1x) = 1/(1+x²)
4. d/dx(csc-1x) = -1/(|x|√x²-1)
5. d/dx(sec-1x) = 1/(|x|√x²-1)
6. d/dx(cot-1x) = -1/(1+x²)

Let us derive each of these derivative formulas.

In the previous section, we have already seen the formulas of derivatives of inverse trigonometric functions. If we observe them carefully, the derivatives neither include trigonometric functions nor include inverse trigonometric functions. Rather they include squares and square roots. Thus, it is difficult to memorize them unless we know how these formulas are derived. We use the process of implicit differentiation (which is the process of using the chain rule when the functions are implicitly defined) to derive the inverse trig derivatives.

Derivative of Arcsin

To find the derivative of arcsin x, let us assume that y = arcsin x. Then by the definition of inverse sine, sin y = x. Differentiating both sides with respect to x,

cos y (dy/dx) = 1

dy/dx = 1/cos y ... (1)

By one of the trigonometric identities, sin2y + cos2y = 1. From this, cos y = √1-sin²y = √1-x².

Substituting this in (1),

dy/dx = 1/√1-x² (or)

d (arcsin x) / dx = 1/√1-x²

Thus, the derivative of arcsin x (or) sin-1x (or) inverse sin x is 1/√1-x².

Derivative of Arccos

To find the derivative of arccos x, let us assume that y = arccos x. Then by the definition of inverse cos, cos y = x. Differentiating both sides with respect to x,

-sin y (dy/dx) = 1

dy/dx = 1/(-sin y) = -1/sin y ... (1)

By one of the trigonometric identities, sin2y + cos2y = 1. From this, sin y = √1-cos²y = √1-x².

Substituting this in (1),

dy/dx = -1/√1-x² (or)

d (arccos x) / dx = 1/√1-x²

Thus, the derivative of arccos x (or) cos-1x (or) inverse cos x is 1/√1-x².

Derivative of Arctan

To find the derivative of arctan x, let us assume that y = arctan x. Then by the definition of inverse tan, tan y = x. Differentiating both sides with respect to x,

sec2y (dy/dx) = 1

dy/dx = 1/(sec2y) ... (1)

By one of the trigonometric identities, sec2y - tan2y = 1. From this, sec2y = 1 + tan2y = 1 + x2.

Substituting this in (1),

dy/dx = 1 / (1 + x2) (or)

d (arctan x) / dx = 1 / (1 + x2)

Thus, the derivative of arctan x (or) tan-1x (or) inverse tan x is 1 / (1 + x2).

Derivative of Arccsc

To find the derivative of arccsc x, let us assume that y = arccsc x. Then by the definition of inverse cosecant, csc y = x. Differentiating both sides with respect to x,

-csc y cot y (dy/dx) = 1

dy/dx = -1/(csc y cot y) ... (1)

By one of the trigonometric identities, csc2y - cot2y = 1. From this, cot2y = csc2y - 1 = x2 - 1. Then cot y = √x²-1.

Also, we have csc y = x.

Substituting this in (1),

dy/dx = -1/(|x|√x²-1)(or)

d (arccsc x) / dx = -1/(|x|√x²-1).

Here, we have written the absolute value sign around x instead of just writing x because if we observe the graph of csc-1x, the slope of the tangent of this curve is always negative. So the derivative of csc-1x must be always negative irrespective of the sign of x. That is why we always write the absolute value sign around x here.

Thus, the derivative of arccsc x (or) csc-1x (or) inverse csc x is -1/(|x|√x²-1).

Derivative of Arcsec

To find the derivative of arcsec x, let us assume that y = arcsec x. Then by the definition of inverse cosecant, sec y = x. Differentiating both sides with respect to x,

sec y tan y (dy/dx) = 1

dy/dx = 1/(sec y tan y) ... (1)

By one of the trigonometric identities, sec2y - tan2y = 1. From this, tan2y = sec2y - 1 = x2 - 1. Then tan y = √x²-1.

Also, we have sec y = x.

Substituting this in (1),

dy/dx = 1/(|x|√x²-1) (or)

d (arcsec x) / dx = 1/(|x|√x²-1).

Here also we have used the absolute value sign as the graph of sec-1x always has tangents with positive slopes and hence the derivative shouldn't be affected by the sign of x.

Thus, the derivative of arcsec x (or) sec-1x (or) inverse sec x is 1/(|x|√x²-1).

Derivative of Arccot

To find the derivative of arccot x, let us assume that y = arccot x. Then by the definition of inverse cot, cot y = x. Differentiating both sides with respect to x,

-csc2y (dy/dx) = 1

dy/dx = -1/(csc2y) ... (1)

By one of the trigonometric identities, csc2y - cot2y = 1. From this, csc2y = 1 + cot2y = 1 + x2.

Substituting this in (1),

dy/dx = -1 / (1 + x2) (or)

d (arccot x) / dx = -1 / (1 + x2)

Thus, the derivative of arccot x (or) cot-1x (or) inverse cot x is -1 / (1 + x2).

Here is a table with derivatives and integrals of inverse trigonometric functions. This will help you to summarize and memorize the difference between the derivatives and integrals of inverse trig functions.

Inverse Trig Function Derivative Integral arcsin x 1/√1-x² x arcsin x + √1-x² + C arccos x -1/√1-x² x arccos x - √1-x² + C arctan x 1/(1+x²) x arctan x - (1/2) ln |x2+1| + C arccsc x -1/(|x|√x²-1) x arccsc x + ln |x + √x²-1| + C arcsec x 1/(|x|√x²-1) x arcsec x - ln |x + √x²-1| + C arccot x -1/(1+x²) x arccot x + (1/2) ln |x2+1| + C

☛Related Topics:

• Differentiation of Trigonometric Functions
• Differentiation
• Derivatives Calculator